下面略提几个方案: 方案一:通过类比扩散方程(cf @赵永峰 、@andrew shen ),可以引入一个有限的声速 : 其中 ,这个方程叫做电报方程,一阶导数项等效于阻尼项,在 是变成傅立叶热传导方程。为了保持能量守恒,需要重新定义热流: 。但这个重新定义意味着,如果温度随时间改变的速度足够快的话,热量将会从低温流向高温。May 29, 17 · 热传导方程建立的全过程,一年四季,春夏秋冬,温度变化无处不在,他到底有什么规律呢?先思考这样一个问题:对于体积相同形状不同的同种物体,什么形状最能减少热量损失的?知乎,中文互联网高质量的问答社区和创作者聚集的原创内容平台,于 11 年 1 月正式上线,以「让人们更好地分享知识、经验和见解,找到自己的解答」为品牌使命。知乎凭借认真、专业、友善的社区氛围、独特的产品机制以及结构化和易获得的优质内容,聚集了中文互联网科技、商业、影视

The Dynamic Thermal Model Of A Building 根据傅里叶热传导方程 楼宇热动态模型可以 Download Scientific Diagram
热传导方程推导
热传导方程推导-热传导方程(抛物型)— 热传导,物质扩散时 的浓度变化规律, 土壤力学 中的渗透方程;前面5节都讲了最基本的分析方法,从今天开始的主线变成了如何构造更有效的差分格式参考书:(1) JW Thomas Numerical Partial Differential Equations_ Finite Difference Methods (1995, Springer)(2) 张强《偏微分方程的有限差分方法》科学出版社,19年1月版。(3) K W Morton, D


怎么用matlab求解二维热传导方程啊能求出第一个方程也好我都快崩溃了 作业 慧海网
Nov 21, 18 · 热传导方程(或称热方程)是一个重要的偏微分方程,它描述一个区域内的温度如何随时间变化。 热传导在三维的各向同性介质里的传播可用以下方程表达: 其中: u =u(t, x, y, z)表温度,它是时间变数t与空间变数(x,y,z)的函数。热传导方程式,热传导方程式(或称热方程)是一个重要的偏微分方程,它描述一个区域内的温度如何随时间变化。热传导在三维的等方向均匀介质里的传播可用方程式表达,其中u =u(t, x, y, z) 表温度,它是时间变量 t 与 空间变量 (x,y,z) 的函数。Laplace方程 (椭圆型)— 稳定的浓度分布, 静电场的电位, 流体的势。
1 什么是热传导方程 热传导方程(heat equation) 以及非齐次热传导方程 其中给定合适的初值与边界条件 这里 为开集 不确定的东西是 而Laplace算子是关于空间 的, 即 在非齐次的方程中 是给定的 下面的主要思路是用调和函数(即位势方程的解)中用到的方法来类比热传导方程(只不过更加复杂), 所以一些思路是相似的 2 基本解(a) (b) (c)有:t1t2t3=Q1R1Q2R2Q3R3稳定热传导时:Q1Q2Q3=Q (35)将式(35)推广到一个层数为n (36)由于Q=t1/R1=t2/R2=t3/R3,可得: t1:t2:t3=R1:R2:R3 (37) 式(37)说明,多层平壁内各层的温度降与热阻成正比。热传导方程是什么类型的偏微分方程 _____ 热传导方程式(或称热方程)是一个重要的偏微分方程,它描述一个区域内的温度如何随时间变化热传导在三维的等方向均匀介质里的传播可用方程式表达,其中u =u(t, x, y, z) 表温度,它是时间变量 t 与 空间变量 (x,y,z) 的函数 /是空间中一点的温度对时间的变化
第四章 热传导方程 关于函数u = u(t;x1;x2;¢¢¢ ;xn)的热传导方程具有下述形式 ut = k4u 其中k是热传导系数,是一个正常数。当n = 1时,导热的绝缘导线中的温度分布满足此 方程;当n = 3时,导热介质中的温度满足上述方程。 此外,在描述扩散过程时,也会 出现同类型的方程。本章我们将介绍这类最典型Dec 14, 18 · 热传导方程如何建立,一年四季,春夏秋冬,温度变化无处不在,他到底有什么规律呢?今天小编就教大家热传导方程如何建立注 1、热传导方程不仅仅描述热传导现象,也可以 刻画分子、气体的扩散等,也称扩散方程; 2、上述边界条件形式上与波动方程的边界条件 一样,但表示的物理意义不一样; 3、热传导方程的初始条件只有一个,而波动方 程有两个初始条件。



热传导方程 Wikiwand



The Dynamic Thermal Model Of A Building 根据傅里叶热传导方程 楼宇热动态模型可以 Download Scientific Diagram
傅里叶定律( 热传导 定律) q= λ ∂T/∂t 表示单位时间内通过单位面积的热量的大小,时温度梯度的反方向 三类边界条件: 第一类边界条件:已知表面温度 第二类边界条件:已知边界上的热流变化规律,即温度沿边界法线方向的导数,称为第二类边界条件,表达式如下: q=λ ∂T/∂t 第三类边界条件:已知边界气流温度及对流换热系数 非稳态 热传导 方程:左边体现温度随时间变化,右边体现了物体内2)计算得到它们,最终确定热传导方程组。具体步骤如下: 1 列出各层满足的热传导方程,确定边界条件,此时方程中含有未知的对流换热系数 hI、hIV 。 2 求解热平衡状态下的热传导方程,由于平衡时皮肤外侧温度已知,由此列出hI 与 hIV 满足的关系式。 3内无粒子源: , 总结:热传导:热量的传递;扩散:粒子的运动,两者本质不同,但满足同一微分方程 _unknown _unknown _unknown _unknown _unknown _unknown _unknown _unknown _1319unknown _unknown _1319unknown _unknown 数



Vook Sshrkqwmm



热传导方程的差分格式原理与matlab实现 随煜而安的专栏 Csdn博客
关键词: 热传导方程, 热传导方程解, 初值问题, 梯度估计, 解析函数 Abstract This paper provesthat the solution of the initial value problem for homogeneous heat conduction equation is an analytical function by the solution formula of the initial value problem for the heat conduction equationThe paper provides the gradient estimation of solutions for homogeneous heat热传导方程(或称热方程)是一个重要的偏微分方程,它描述一个区域内的温度如何随时间变化。 For faster navigation, this Iframe is preloading the Wikiwand page for 热传导方程热传导方程就是温度所满足的偏微分方程,它的解给出任意时刻物体内的温度分布。 为了建立热导方程,我们首先介绍热导系统置于 x 轴,考查系统在任意 x 处的横截面上的一个单位面积,设热流沿 x 轴方向传递, x 处的温度为 u ( x ),温度梯度为 du ( x )/ dx 。



动画直观解释一个重要的偏微分方程 热传导方程 网易公开课



Vnt7aurwvh Aem
Jun 28, 04 · 热传导,是热能从高温向低温部分转移的过程,是 一个分子向另一个分子传递振动能的结果。 各种材料的热传导性能不同,传导性能好的,如金属,还包括了自由电子的移动,所以传热速度快,可以做热交换器材料,而金屬傳導能力依次爲銀>銅>金>鋁;传导性能不好的,如石棉,可以做热第四章 热传导方程 关于函数u = u(t;x1;x2;¢¢¢ ;xn)的热传导方程具有下述形式 ut = k4u 其中k是热传导系数,是一个正常数。当n = 1时,导热的绝缘导线中的温度分布满足此 方程;当n = 3时,导热介质中的温度满足上述方程。此外,在描述扩散过程时,也会传热学,导热微分方程推导过程中的这个式子如何理解? (最上面的 10 热传导方程式的介绍 10;



热传导方程 第1页 图说健康



004icbc
热传导方程热传导方程pdf,第二章 热传导方程 齐海涛 山东大学威海分校数学与统计学院 Email htqisdu@ September28, 11 目录 1 热传导方程及其定解问题的导出 2 2 初边值问题的分离变量法 4 3 柯西问题 7 4 极值原理、定解问题解的唯一性和稳定性 10 5 解的渐近性态 12 1 1 热传导方程及其定解问题的导出 例1第一章 热传导方程 1 推导一维杆的热传导方程:从微分及积分角度分别进行了推导 2 初值和边界条件:初值是与时间相关、边值与空间相关 3 二维及三维热传导方程推导:从积分角度推导,得到泊松方程和拉普拉斯方程 4 拉普拉斯算子的各种形式:在直角坐标系、柱坐标系和球坐标系下推导拉普拉斯算子第一章 热传导方程 目录如下: 1 推导一维杆的热传导方程:从微分及积分角度分别进行了推导 2 初值和边界条件:初值是与时间相关、边值与空间相关 3 二维及三维热传导方程推导:从积分角度推导,得到泊松方程和拉普拉斯方程 4


基于偏微分方程的高温作业专用服装设计模型 科学猫



熱傳導方程式 热传导方程 或稱熱方程 是一個重要的偏微分
折叠 热扩散方程 在最一般的热传导中,温度随时间和三个空间坐标而变化,且伴有 热量 产生或者消耗 (例如,反应热)。 这时的热传导称为三维 非定态 热传导,可用热扩散方程 (Heat Equation)描述 式中 τ 为时间;热传导 术语拼音 rè chuán dǎo 术语英文 heat conduction 术语定义 所属学科 统计物理学 术语审定 物理学名词审定委员会 见载刊物 《物理学名词(第二版)》 科学出版社 发布时间 1996年1、热传导方程不仅仅描述热传导现象,也可以 刻画分子、气体的扩散等,也称扩散方程; 4、除了三维热传导方程外,物理上,温度的分布在同一个界面上是相同的,可得一维热传导方 当我们研究物理中的各类现象,如振动、热传导、扩散等的稳定过程时,由于表达该物理过程的物 如果我们考虑的是一个稳定的热场,则可以得到不随时间变化而变化的温度 所满足的方



有限差分法之热传导方程的求解 快资讯


数学物理方程课程教学大纲2400字 范文118
传热方程和热平衡方程的单位一样吗? 不是有个是瓦一个是焦吗,为 热力学公式 12一维热传导方程的 CrankNicolson 格式 发表于 0527 更新于 1221 分类于 Numerical PDEs 阅读次数: 一维热传导方程 CrankNicolson 格式的 MATLAB 编程实现 。非齐次热传导方程 : 当物体体积很大,考虑时间很短和较小范围内的温度变化情况,边界条件所产生的影响可以忽略,这时就不放吧考察的物体视为充满整个空间,而定解问题就成为 柯西问题 ,此时初始条件为 扩散方程 称为 扩散系数 ,总取正值 扩散方程为 如果 是常数,记 ,扩散方程就化为与热传导方程完全相同的形式



热传导方程扩散方程为什么有空间一阶导数的项 业百科



扩散方程 热传导问题 能量定律 傅里叶热传导定律 拉普拉斯方程 偏微分方程 三 码农家园
X 、 y 、 z 为 坐标轴;数学物理方程第二章 热传导方程ppt,数学物理方程 第二章 热传导方程 §11 热传导方程的导出 §1 热传导方程及其定解问题的导出 §12 定解问题的提法 §13 扩散方程 §11 热传导方程的导出 物理背景:热传导和扩散等物理现象。 因为温差而引起的热量输运过程称为热传导。4)能量守恒定律得到热传导方程 因为t1、t2与区域D是任意的,且被积函数是连续函数,所以G内任意一点任意时刻均有 化简,即得到热传导方程一般形式 无热源: 一维有热源: 二维有热源: Laplace方程 拉普拉斯方程 Laplace 算子;



隐方程求解一维抛物型方程 热传导方程 Nekocyan的博客 Csdn博客



基于热传导方程的高温服装模型设计 参考网



不均匀介质中的均匀化稳恒热传导方程 知网百科



004icbc



2d热传导练习 Games1 高级物理引擎实战 Taichi


热传导方程之显示差分算法 Python源码 条件


数学物理方程习题解 谷超豪 第二章热传导方程 文档库



18国赛数学建模笔记 尚码园



遠得要命的數學王國 熱傳導方程與傅立葉變換 فيسبوك



数值方法3 偏微分方程1使用有限差分法解一维热传导 扩散 方程 哔哩哔哩 つロ干杯 Bilibili



傅里叶热传导方程


过桥米线里的肉片热传导模型 科学松鼠会 财新博客 新世纪的常识传播者 财新网



Cnb 高速铁路板式无砟轨道结构实时温度分布数据的快速确定方法 Google Patents



有限差分法求解一维热传导方程 学习笔记



热传导方程 第1页 图说健康



数学物理方程 第二章热传导方程 知乎


Chapter 11 偏微分方程 Some Notes On Mathematics



第二章热传导动方程第一节热传导方程的导出和定解条件一 热传导方程的导出 模型 问题 Ppt Download



Matlab热传导方程差分方法的实现 365bet亚洲版官网 日博体育开户


第三章热传导方程1 4 基本解 哔哩哔哩 つロ干杯 Bilibili


一维热传导方程的推导 论文 绿色文库网



第一章热传导方程 简单快乐 Csdn博客



北邮偏微分方程10学年第二学期期末试卷a卷及答案 申请方



热传导 搜索结果 哔哩哔哩弹幕视频网 つロ乾杯 Bilibili



第一章热传导方程 Simppy 博客园



热传导方程建立的全过程 百度经验



数值计算 四十一 一维热传导方程的求解 知乎


2 2 2 一维热传导方程 51cto Com



网易公开课 上好人生每一课



热传导方程与扩散方程ppt下载 Ppt模板 爱问共享资料



有限差分法之热传导方程的求解 快资讯


一维热传导方程的推导 论文 绿色文库网



第二章 热传导方程 Ppt 第二章热传导动方程第一节热传导方程的导出和定解条 一 热传导方程的导出 Y Z Course Hero


Fenics入门 二 热传导方程 一 知乎


头条文章


计算热传导方程的精确特征模式 Wolfram语言11 的新功能



2 2 2 一维热传导方程 51cto Com



定解问题 360图片



数学物理方程 2 热传导方程 1 2课件ppt下载 Ppt模板 爱问共享资料


毕业设计 论文 二维热传导方程有限差分法的matlab实现 沃文网wodocx Com



Cad Cam Cae基础 三 材料加工cae技术基础 码农家园


一维热传导方程 爱学术



基于热传导方程的高温服装模型设计 参考网



一维热传导方程的差分法 参考网


Black Scholes Merton Pde And Heat Equation Bsm偏微分方程和热传导方程 Matpij



第二章热传导动方程第一节热传导方程的导出和定解条件一 热传导方程的导出 模型 问题 Ppt Download



利用蒙特卡罗法求解热传导方程 简书



Scipy一维热传导方程的求解 简书



热传导方程的物理意义 三人行教育网 Www 3rxing Org
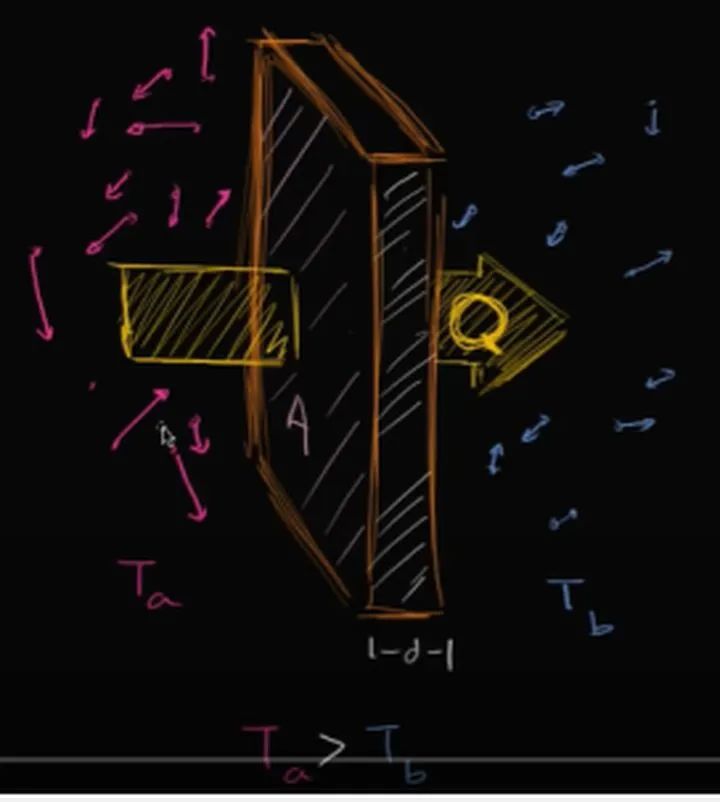


游戏流体力学基础及unity代码 一 热传导方程 Marszhou的个人空间 Oschina 中文开源技术交流社区



熱傳導方程式 维基百科 自由的百科全书



数学物理方程 第二章热传导方程 知乎
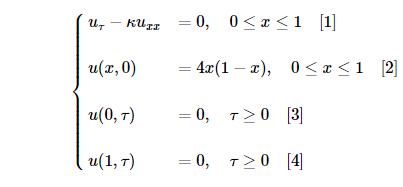


量化分析师的python日记 第10天q Quant兵器谱 之偏微分方程1 Python 量化交易教程



偏微分 新人首单优惠推荐 淘宝海外


Teesim Fem02 直接法建立连续系统的数学模型



量化分析师的python日记 第10天q Quant兵器谱 之偏微分方程1 自由汇


热传导方程之显示差分算法 Python源码 条件


Matlab 求解偏微分方程 有偿 仿真模拟 小木虫 学术科研互动社区


怎么用matlab求解二维热传导方程啊能求出第一个方程也好我都快崩溃了 作业 慧海网



Ppt 第二篇数学物理方程powerpoint Presentation Free Download Id


第四章 偏微分方程的有限差分法 Ppt 十八文库



广义函数新款 广义函数21年新款 京东



热传导方程的柯西问题 知网百科



Ppt 第二篇数学物理方程powerpoint Presentation Free Download Id


12月10日学术报告 热力学定律与热传导方程的性质


细览页面



第一章热传导方程 Simppy 博客园



利用fourier变换求解热传导方程的定解问题 金启胜 Pdf 第31 卷第3 期上 师范学院学报vol 31 No 3 Course Hero


Advanced Engineering Mathematics



Chapter 11 偏微分方程 Some Notes On Mathematics



18国赛数学建模笔记 尚码园


一维热传导方程数值解法及matlab实现分离变量法和有限差分法 沃文网wodocx Com


一维热传导方程 爱学术
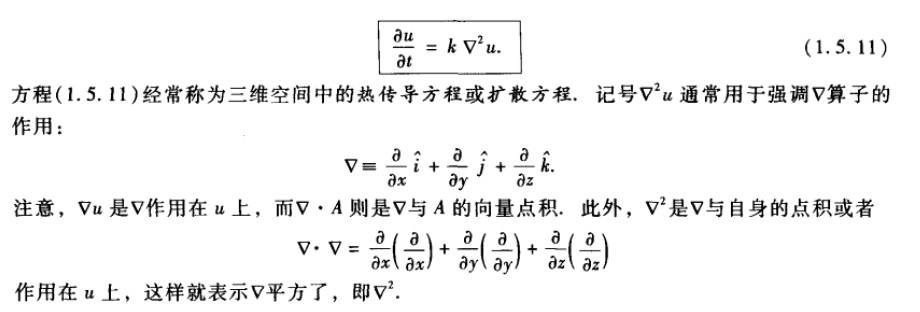


第一章热传导方程 Simppy 博客园



7 4 3 热传导方程的定解问题 Youtube


第二章 热传导方程 图文 百度文库



0 件のコメント:
コメントを投稿